Proceso de aprendizaje automático supervisado
Una introducción la automatización del aprendizaje supervisado. Python + Pytorch
Partimos de una realidad que queremos estudiar.
Buscando patrones construimos modelos que simplifiquen esta realidad y nos ayuden a sacar ventajas.
Los modelos buscan el equilibrio entre representar bien la realidad y la simplicidad de uso.
Elementos:
- datos: valores sacados de la realidad que alimentan el modelo
- parámetros: valores que se pueden variar para ajustar el modelo
- error: mide el grado de ajuste de nuestro modelo a los datos
Partiendo de un modelo inicial, el objetivo será optimizarlo (entrenarlo, ajustarlo) a través de la variación de los parámetros buscando el mínimo error.
Dentro del aprendizaje automático (machine learning) hay tres ramas diferenciadas:
- aprendizaje supervisado: se tiene datos etiquetados (clasificados), sabemos el objetivo buscado
- aprendizaje no supervisado: se busca sacar conocimiento con datos no etiquetados, se desconoce a priori el objetivo.
- aprendizaje reforzado: se establece un sistema de refuerzos y penalizaciones para llegar al objetivo
Nosotros comenzaremos por el aprendizaje supervisado escogiendo lo más sencillo, un modelo lineal.
Regresión lineal simple: una variable
Tenemos sólo una variable x de entrada (v. independiente), y se busca un resultado y que depende de la anterior. Existe una relación lineal entre ambas, por lo que se representa como una línea:
y = b + w1 * x
b y w1 son los parámetros: el sesgo y la pendiente de la línea
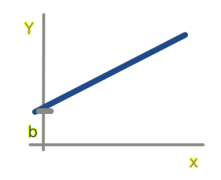
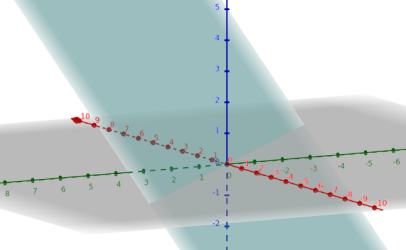
Tanto para regresion lineal simple como múltiple tendremos unos datos sacados de la realidad y queremos encontrar un modelo (una línea, plano,...) que se aproxime a ellos:
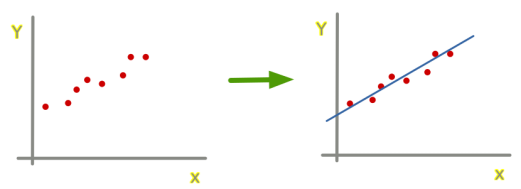
Para cada punto podemos calcular el error (distancia) que hay entre el valor real y la predicción:
error = Y real - Y estimado
El error (coste) del modelo será la media de estas distancias:
error_media_abs = ((y_real-y_estimado)).abs().mean()
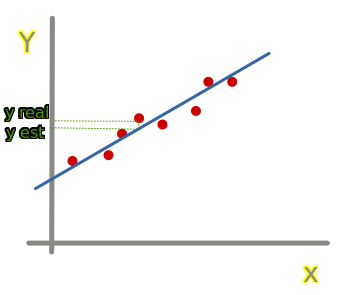
Aunque, se suele utilizar la raiz cuadrada del error medio cuadrático (MSE) porque penaliza más cuanto mayor sea el error:
error_mse = ((y_real-y_estimado)**2).mean().sqrt()
F.l1_loss(y_real.float(),y_estimado)
F.mse_loss(y_real,y_estimado).sqrt()
Una vez tenemos el modelo y la función de error, iremos dando valores a los parámetros w y b buscando el menor error hasta encontrar el modelo que mejor se ajuste a la realidad.
Queremos que ese ajuste de parámetros se realice de forma autónoma. Para ello tenemos la herramienta desceso del gradiente.
La técnica de descenso del gradiente consiste en moverse por la función de error buscando el punto donde se minimiza. Para ello, en cada posición, busca la dirección en la que se reduce más el error. Esto se obtiene con la derivada parcial en el punto respecto de cáda parámetro (el gradiente de la función), que es la pendiente de la curva.
Una vez obtenida la dirección en que hay que moverse se recalculan los parámetros de la siguiente forma:
w := w - gradiente(w) * lr
'lr' es la tasa de aprendizaje, que define el tamaño del paso que se realizará. Si es demasiado pequeño se necesitará mucho tiempo para alcanzar el mínimo y si es muy grande seguramente se pasará de largo sin llegar al mínimo.
funcion_error.backward()
parametros.grad
Ahora ya podemos preparar el algoritmo de aprendizaje automático. Los pasos serán:
1- Cargar los datos y escoger el modelo
2- Inicializar los parámetros: se suele hacer de forma aleatoriaparametros = torch.randn(num_parametros).requires_grad_()
3- Calcular la predicciones
4- Calcular el error (coste) error = mse(prediciones, valores_reales)
5- Calcular el gradiente
6- Realizar el paso, modificación de los parámetroslr = 1e-5
parametros.data -= lr * parametros.grad.data
parametros.grad = None
7- Repetir el proceso (punto 3) las veces necesarias