Guía rápida de Machine Learning con Python
Guía de referencia rápida de aprendizaje automático con Python
- Introducción
- Los pasos a seguir para obtener un software de aprendizaje automático son:
- 1 - Recoger los datos
- 2 - Preparar los datos
- 2.1 - Exploración de los datos
- Visualización
- 2.2- Tratamiento de valores que faltan
- 2.3.- Variables numéricas y categóricas
- 2.3- Codificaciones de caracteres
- 2.4- Escalado y normalizado
- 2.5- Fechas
- 2.6- Entradas de datos inconsistentes
- 2.7- Ingeniería de datos
- Separar los datos para entrenar y validar
- 3- Seleccionar el modelo
- 4- Entrenar el modelo
- 5- Evaluar el modelo
- 6- Ajustar los parámetros
- 7- Generar la predicciones
- Otros puntos a tener en cuenta
Introducción
Machine learning (aprendizaje automático) es una parte de la Inteligencia Artificial.
Consiste en un nuevo paradigma de desarrollo de software. En lugar de decir al ordenador qué debe hacer con los datos, el desarrollador proporciona datos para que el ordenador 'aprenda' a realizar una tarea específica.
Es una herramienta muy útil para realizar tareas complejas en las que el ser humano prevalecía sobre las máquinas hasta hace poco tiempo, como el reconocimiento de imagenes. Además, se adapta muy bien a entornos cambiantes al contrario que el software convencional.
El un software altamente dependiente de datos.
En los últimos años, gracias a la recolección masiva de datos y al uso de GPUs (tarjetas gráficas) se ha avanzado mucho en el uso de redes neuronales artificiales, apareciendo una subcategoría llamada Deep Learning (aprendizaje profundo) que se basa en el uso de redes neuronales de múltiples capas.
Tareas: objetivos a resolver
-
Predictivas (aprendizaje supervisado):
- Clasificación: se obtiene un valor categórico
- Regresión: se obtiene una valor numérico
-
Descriptivas (aprendizaje no supervisado):
- Clustering: encontrar grupos
- Analisis exploratorio:
- Reglas de asociación,dependencias funcionales (var. categóricas)
- Análisis de correlación, dispersión, multivariable (var. numéricas)
Técnicas: algoritmos/procedimientos usados. Ejemplos según tarea a realizar:
| Técnica | Clasificación | Regresión | Clustering | Análisis exploratorio |
|---|---|---|---|---|
| Redes neuronales | x | x | x | - |
| Árboles de decisión | x | x | x | - |
| Regresión lineal | - | x | - | - |
| Regresión logística | x | - | - | - |
| K-Means | x | - | x | - |
| A priori | - | - | - | x |
| Análisis factorial | - | - | - | x |
| Análisis multivariable | - | - | - | x |
| K-NN (vecinos cercanos) | x | - | x | - |
| Clasificadores bayesianos | x | x | - | - |
Herramientas: ayudan a utilizar las técnicas.
-
Lenguajes más usados:
- Python + librerias (scikit-learn, ...)
- R
-
Suites: software más visual y adaptado
- Open source:
- Comerciales:
- Nube:
import pandas as pd
datos = pd.read_csv(ruta_archivo) # cargar datos desde tabla en archivo csv
datos.describe() # imprime resumen de los datos
datos.columns # imprime lista de las columnas
datos.head() # imprime lista de las 5 primeras muestras de la tabla
datos.tail() # imprime lista de las 5 últimas muestras de la tabla
datos_filtrados = datos.dropna(axis=0) # elimina datos na (no available - no disponibles)
X_full.dropna(axis=0, subset=['SalePrice'], inplace=True) # Eliminar filas sin datos destino,
# elegir la columna que deseamos estimar en nuestro modelo
y = X_full.SalePrice
# elegir las columnas que se pasarán al modelo
# opción 1: quitar la columna destino
X_full.drop(['SalePrice'], axis=1, inplace=True)
# opción 2: elegir sólo algunas columnas
datos_features = ['Rooms', 'Bathroom','Lattitude', 'Longtitude']
X = datos[datos_features]
colors = ["lightcoral", "sandybrown", "darkorange", "mediumseagreen",
"lightseagreen", "cornflowerblue", "mediumpurple", "palevioletred",
"lightskyblue", "sandybrown", "yellowgreen", "indianred",
"lightsteelblue", "mediumorchid", "deepskyblue"]
fig, ax = plt.subplots(figsize=(5, 5))
pie = ax.pie([len(train), len(test)],
labels=["Train dataset", "Test dataset"],
colors=["salmon", "teal"],
textprops={"fontsize": 15},
autopct='%1.1f%%')
ax.axis("equal")
ax.set_title("Dataset length comparison", fontsize=18)
fig.set_facecolor('white')
plt.show();
fig, ax = plt.subplots(figsize=(16, 8))
bars = ax.hist(train["target"],
bins=100,
color="palevioletred",
edgecolor="black")
ax.set_title("Target distribution", fontsize=20, pad=15)
ax.set_ylabel("Amount of values", fontsize=14, labelpad=15)
ax.set_xlabel("Target value", fontsize=14, labelpad=10)
ax.margins(0.025, 0.12)
ax.grid(axis="y")
plt.show();
cat_features = ["cat" + str(i) for i in range(10)]
num_features = ["cont" + str(i) for i in range(14)]
df = pd.concat([train[num_features], test[num_features]], axis=0)
columns = df.columns.values
# Calculating required amount of rows to display all feature plots
cols = 3
rows = len(columns) // cols + 1
fig, axs = plt.subplots(ncols=cols, nrows=rows, figsize=(16,20), sharex=False)
# Adding some distance between plots
plt.subplots_adjust(hspace = 0.3)
# Plots counter
i=0
for r in np.arange(0, rows, 1):
for c in np.arange(0, cols, 1):
if i >= len(columns): # If there is no more data columns to make plots from
axs[r, c].set_visible(False) # Hiding axes so there will be clean background
else:
# Train data histogram
hist1 = axs[r, c].hist(train[columns[i]].values,
range=(df[columns[i]].min(),
df[columns[i]].max()),
bins=40,
color="deepskyblue",
edgecolor="black",
alpha=0.7,
label="Train Dataset")
# Test data histogram
hist2 = axs[r, c].hist(test[columns[i]].values,
range=(df[columns[i]].min(),
df[columns[i]].max()),
bins=40,
color="palevioletred",
edgecolor="black",
alpha=0.7,
label="Test Dataset")
axs[r, c].set_title(columns[i], fontsize=14, pad=5)
axs[r, c].tick_params(axis="y", labelsize=13)
axs[r, c].tick_params(axis="x", labelsize=13)
axs[r, c].grid(axis="y")
axs[r, c].legend(fontsize=13)
i+=1
# plt.suptitle("Numerical feature values distribution in both datasets", y=0.99)
plt.show();
df = pd.concat([train[cat_features], test[cat_features]], axis=0)
columns = df.columns.values
# Calculating required amount of rows to display all feature plots
cols = 3
rows = len(columns) // cols + 1
fig, axs = plt.subplots(ncols=cols, nrows=rows, figsize=(16,20), sharex=False)
# Adding some distance between plots
plt.subplots_adjust(hspace = 0.2, wspace=0.25)
# Plots counter
i=0
for r in np.arange(0, rows, 1):
for c in np.arange(0, cols, 1):
if i >= len(cat_features): # If there is no more data columns to make plots from
axs[r, c].set_visible(False) # Hiding axes so there will be clean background
else:
values = df[cat_features[i]].value_counts().sort_index(ascending=False).index
bars_pos = np.arange(0, len(values))
if len(values)<4:
height=0.1
else:
height=0.3
bars1 = axs[r, c].barh(bars_pos+height/2,
[train[train[cat_features[i]]==x][cat_features[i]].count() for x in values],
height=height,
color="teal",
edgecolor="black",
label="Train Dataset")
bars2 = axs[r, c].barh(bars_pos-height/2,
[test[test[cat_features[i]]==x][cat_features[i]].count() for x in values],
height=height,
color="salmon",
edgecolor="black",
label="Test Dataset")
y_labels = [str(x) for x in values]
axs[r, c].set_title(cat_features[i], fontsize=14, pad=1)
axs[r, c].set_xlim(0, len(train["id"])+50)
axs[r, c].set_yticks(bars_pos)
axs[r, c].set_yticklabels(y_labels)
axs[r, c].tick_params(axis="y", labelsize=10)
axs[r, c].tick_params(axis="x", labelsize=10)
axs[r, c].grid(axis="x")
axs[r, c].legend(fontsize=12)
axs[r, c].margins(0.1, 0.02)
i+=1
#plt.suptitle("Categorical feature values distribution in both datasets", y=0.99)
plt.show();
Check if the datasets have different amount of categories in categorical features
bars_pos = np.arange(len(cat_features))
width=0.3
fig, ax = plt.subplots(figsize=(14, 6))
# Making two bar objects. One is on the left from bar position and the other one is on the right
bars1 = ax.bar(bars_pos-width/2,
train[cat_features].nunique().values,
width=width,
color="darkorange", edgecolor="black")
bars2 = ax.bar(bars_pos+width/2,
train[cat_features].nunique().values,
width=width,
color="steelblue", edgecolor="black")
ax.set_title("Amount of values in categorical features", fontsize=20, pad=15)
ax.set_xlabel("Categorical feature", fontsize=15, labelpad=15)
ax.set_ylabel("Amount of values", fontsize=15, labelpad=15)
ax.set_xticks(bars_pos)
ax.set_xticklabels(cat_features, fontsize=12)
ax.tick_params(axis="y", labelsize=12)
ax.grid(axis="y")
plt.margins(0.01, 0.05)
Checking if test data doesn't contain categories that are not present in the train dataset
for col in cat_features:
print(set(train[col].value_counts().index) == set(test[col].value_counts().index))
feature correlation.
df = train.drop("id", axis=1)
# Encoding categorical features with OrdinalEncoder
for col in cat_features:
encoder = OrdinalEncoder()
df[col] = encoder.fit_transform(np.array(df[col]).reshape(-1, 1))
# Calculatin correlation values
df = df.corr().round(2)
# Mask to hide upper-right part of plot as it is a duplicate
mask = np.zeros_like(df)
mask[np.triu_indices_from(mask)] = True
# Making a plot
plt.figure(figsize=(14,14))
ax = sns.heatmap(df, annot=True, mask=mask, cmap="RdBu", annot_kws={"weight": "normal", "fontsize":9})
ax.set_title("Feature correlation heatmap", fontsize=17)
plt.setp(ax.get_xticklabels(), rotation=90, ha="right",
rotation_mode="anchor", weight="normal")
plt.setp(ax.get_yticklabels(), weight="normal",
rotation_mode="anchor", rotation=0, ha="right")
plt.show();
feature vs target.
columns = train.drop(["id", "target"], axis=1).columns.values
# Calculating required amount of rows to display all feature plots
cols = 4
rows = len(columns) // cols + 1
fig, axs = plt.subplots(ncols=cols, nrows=rows, figsize=(16,20), sharex=False)
# Adding some distance between plots
plt.subplots_adjust(hspace = 0.3)
i=0
for r in np.arange(0, rows, 1):
for c in np.arange(0, cols, 1):
if i >= len(columns):
axs[r, c].set_visible(False)
else:
scatter = axs[r, c].scatter(train[columns[i]].values,
train["target"],
color=random.choice(colors))
axs[r, c].set_title(columns[i], fontsize=14, pad=5)
axs[r, c].tick_params(axis="y", labelsize=11)
axs[r, c].tick_params(axis="x", labelsize=11)
i+=1
# plt.suptitle("Features vs target", y=0.99)
plt.show();
¿Por qué faltan los valores?
- No existen -> no hacer nada, no tiene sentido intentar estimarlos
- No han sido grabados -> se puede intentar estimarlos, basándonos en otros valores de la tabla
Revisar cada columna para averiguar cual es la mejor aproximación.
missing_val_count_by_column = X_train.isnull().sum() # Número de valores faltantes en cada columna de datos de entrenamiento
print(missing_val_count_by_column[missing_val_count_by_column > 0])
# how many total missing values do we have?
total_cells = np.product(X_train.shape)
total_missing = missing_val_count_by_column.sum()
# percent of data that is missing
percent_missing = (total_missing/total_cells) * 100
train.isna().sum().sum(), test.isna().sum().sum()# Checking if there are missing values in the datasets
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()] # recopilar columnas con valores que faltan
# eliminar columnas con valores que faltan
reduced_X_train = X_train.drop(cols_with_missing, axis=1)
reduced_X_valid = X_valid.drop(cols_with_missing, axis=1)
reduced_X_train= X_train.dropna() # Otra opción: elimina todas las columnas con datos no disponibles
from sklearn.impute import SimpleImputer
# Imputación
my_imputer = SimpleImputer(strategy='median') # mean, median, most_frequent, constant
imputed_X_train = pd.DataFrame(my_imputer.fit_transform(X_train), index=range(1, X_train.shape[0] + 1),
columns=range(1, X_train.shape[1] + 1))
imputed_X_valid = pd.DataFrame(my_imputer.transform(X_valid), index=range(1, X_valid.shape[0] + 1),
columns=range(1, X_valid.shape[1] + 1))
# Imputación quitó los nombres de columnas, volver a ponerlos
imputed_X_train.columns = X_train.columns
imputed_X_valid.columns = X_valid.columns
X_train.fillna(0) # reemplazar con 0 los NA
X_train.fillna(method='bfill', axis=0).fillna(0) # reemplaza también los valores que vienen después en la misma columna
X_train_plus = X_train.copy() # Hacer una copia para evitar cambiar los datos originales (al imputar)
X_valid_plus = X_valid.copy()
# Hacer nuevas columnas que indiquen lo que se imputará.
for col in cols_with_missing:
X_train_plus[col + '_was_missing'] = X_train_plus[col].isnull()
X_valid_plus[col + '_was_missing'] = X_valid_plus[col].isnull()
# Imputación
my_imputer = SimpleImputer()
imputed_X_train_plus = pd.DataFrame(my_imputer.fit_transform(X_train_plus))
imputed_X_valid_plus = pd.DataFrame(my_imputer.transform(X_valid_plus))
# Imputación quitó los nombres de columnas, volver a ponerlos
imputed_X_train_plus.columns = X_train_plus.columns
imputed_X_valid_plus.columns = X_valid_plus.columns
from sklearn.feature_selection import VarianceThreshold
X = [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]]
selector = VarianceThreshold(threshold=0.0)
selector.fit_transform(X)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import QuantileTransformer
rng = np.random.RandomState(0)
X = np.sort(rng.chisquare(4, 100), axis=0).reshape(-1, 1)
qt = QuantileTransformer(n_quantiles=10, output_distribution='normal', random_state=0)
Xt = qt.fit_transform(X)
2.3.2.- Variables categóricas
Toman un número limitado de valores. Necesitan ser preprocesados antes de usarlos en los modelos.
Variables Ordinales -> deja la variable como está y añade otra con One-Hot encoding (atraparás efectos ordinales lineales y no lineales)
Variables baja cardinalidad (2-255) -> usar One-hot encoding
Variables alta cardinalidad (+ 255) -> usar Label encoding + capa de incrustación(embedding layer) si se usa red neuronal.
object_cols = [col for col in X_train.columns if X_train[col].dtype == "object"]
# para obtener lista de variables categóricas
print(object_cols)
good_label_cols = [col for col in object_cols if # Columnas que se pueden codificar con etiquetas de forma segura
set(X_train[col]) == set(X_valid[col])]
# Columnas problemáticas que se eliminarán del conjunto de datos
bad_label_cols = list(set(object_cols)-set(good_label_cols))
# Aplicar codificador de etiquetas
label_encoder = LabelEncoder()
for col in good_label_cols:
label_X_train[col] = label_encoder.fit_transform(X_train[col])
label_X_valid[col] = label_encoder.transform(X_valid[col])
object_nunique = list(map(lambda col: X_train[col].nunique(), object_cols))
# Obtener el número de entradas únicas en cada columna con datos categóricos
d = dict(zip(object_cols, object_nunique))
# Imprimirc el número de entradas únicas por columna, en orden ascendente
sorted(d.items(), key=lambda x: x[1])
drop_X_train = X_train.select_dtypes(exclude=['object'])
drop_X_valid = X_valid.select_dtypes(exclude=['object'])
from sklearn.preprocessing import OrdinalEncoder
# Hacer una copia para evitar cambiar los datos originales
label_X_train = X_train.copy()
label_X_valid = X_valid.copy()
# Aplicar codificador ordinal a cada columna con datos categóricos
ordinal_encoder = OrdinalEncoder()
label_X_train[object_cols] = ordinal_encoder.fit_transform(X_train[object_cols])
label_X_valid[object_cols] = ordinal_encoder.transform(X_valid[object_cols])
# De esta forma ha asigando valores aleatorios a las categorías. Asignar un orden puede mejorar el modelo.
2.3.2.3- Codificación One-Hot
Crea una columna por cada valor único e indica la presencia o no de ese valor. No asume un orden en las categorías. Variables nominales. No funciona bien si hay muchas categorias. Usar si hay 15 como máximo.
- handle_unknown='ignore': para evitar errores cuando los datos de validación contienen clases que no están representadas en los datos de entrenamiento
- sparse=False: asegura que las columnas codificadas se devuelvan como una matriz densa (en lugar de una matriz dispersa)
Suele ser la mejor aproximación.
from sklearn.preprocessing import OneHotEncoder
# Columnas que se codificarán one-hot (como máximo 10 categorias)
low_cardinality_cols = [col for col in object_cols if X_train[col].nunique() < 10]
# Columnas que se eliminarán
high_cardinality_cols = list(set(object_cols)-set(low_cardinality_cols))
# Aplicar codificador one-hot a cada columna con datos categóricos
OH_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
OH_cols_train = pd.DataFrame(OH_encoder.fit_transform(X_train[low_cardinality_cols]))
OH_cols_valid = pd.DataFrame(OH_encoder.transform(X_valid[low_cardinality_cols]))
# codificador one-hot elimina; ponerlo de nuevo
OH_cols_train.index = X_train.index
OH_cols_valid.index = X_valid.index
# Eliminar columnas categóricas (se reemplazarán con codificación one-hot)
num_X_train = X_train.drop(object_cols, axis=1)
num_X_valid = X_valid.drop(object_cols, axis=1)
# añadir columnas codificadas one-hot a variables numéricas
OH_X_train = pd.concat([num_X_train, OH_cols_train], axis=1)
OH_X_valid = pd.concat([num_X_valid, OH_cols_valid], axis=1)
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder
import pandas as pd
df = pd.DataFrame({'col1': ['red color', 'blue color', 'green color']})
le = LabelEncoder()
le.fit_transform(df['col1'])
dictionary_length = len(le.classes_)
tf.keras.layers.Embedding( input_dim, output_dim)
import chardet
after = before.encode("utf-8", errors="replace")
Detectar codificación automáticamente
with open("../data.csv", 'rb') as rawdata:
result = chardet.detect(rawdata.read(10000)) # en este caso lee 10.000 caracteres
print(result['encoding'])
datos = pd.read_csv("./data.csv", encoding=result['encoding']) # guardar en archivo
from mlxtend.preprocessing import minmax_scaling
scaled_data = minmax_scaling(original_data, columns=[0]) # escalado entre 0 y 1
numerical_cols = [col for col in useful_features if 'cont' in col]
scaler = preprocessing.StandardScaler()
xtrain[numerical_cols] = scaler.fit_transform(xtrain[numerical_cols])
xvalid[numerical_cols] = scaler.transform(xvalid[numerical_cols])
xtest[numerical_cols] = scaler.transform(xtest[numerical_cols])
from scipy import stats
# obtener el índice de todos los valores positivos (Box-Cox solo acepta valores positivos)
index_of_positives = datos.pledged > 0
# get only positive pledges (using their indexes)
valores_positivos = datos.columnaA.loc[index_of_positives]
# normalizar con Box-Cox
norm_valores = pd.Series(stats.boxcox(valores_positivos)[0],
name='columnaA', index=valores_positivos.index)
normalizer = preprocessing.Normalizer()
import numpy as np
from sklearn.preprocessing import RobustScaler
X = [[ 1., -2., 2.], [ -2., 1., 3.], [ 4., 1., -2.]]
rsc= RobustScaler()
rsc.fit_transform(X)
for col in numerical_cols:
df[col]=np.log1p(df[col])
df_test[col]=np.log1p(df_test[col])
import pandas as pd
import datetime
datos['nueva_columna'] = pd.to_datetime(datos['fecha'], format="%d/%m/%y",infer_datetime_format=True)
# infer_datetime_format=True : usar sólo cuando sea extrictamente necesario
dia_mes = datos['nueva_columna'].dt.day # día del mes
# quitar los datos no disponibles
dia_mes = dia_mes .dropna()
# plot the day of the month
sns.distplot(dia_mes, kde=False, bins=31)
date_lengths = datos.Date.str.len() # comprobar la longitud de los valores
date_lengths.value_counts()
indices = np.where([date_lengths == 24])[1]
print('Indices con datos corruptos:', indices)
datos.loc[indices]
Using the type datetime64, you can easily extract the time parts
import pandas as pd
df = pd.DataFrame({'col1': ['02/03/2017', '02/04/2017', '02/05/2017’]})
df['col1'] = df['col1'].astype('datetime64[ns]')
df.col1.dt.year, df.col1.dt.month, df.col1.dt.weekofyear,\
df.col1.dt.day, df.col1.dt.dayofyear, df.col1.dt.dayofweek
Using sine and cosine transformations, create periodic features
import pandas as pd
import numpy as np
df = pd.DataFrame({'col1': ['02/03/2017', '02/04/2017', '02/05/2017']})
df['col1'] = df['col1'].astype('datetime64[ns]')
cycle = 7
df['weekday_sin'] = np.sin(2 * np.pi * df['col1'].dt.dayofweek / cycle)
df['weekday_cos'] = np.cos(2 * np.pi * df['col1'].dt.dayofweek / cycle)
professors['Country'] = professors['Country'].str.lower() # convertir a minúsculas
professors['Country'] = professors['Country'].str.strip() # quitar espacios en blanco, al principio y fin
# coger los 10 más cercanos a south korea
countries = professors['Country'].unique()
matches = fuzzywuzzy.process.extract("south korea", countries, limit=10, scorer=fuzzywuzzy.fuzz.token_sort_ratio)
def replace_matches_in_column(df, column, string_to_match, min_ratio = 47):
# lista de valores únicos
strings = df[column].unique()
# coger los 10 más cercanos a la cadena de entrada
matches = fuzzywuzzy.process.extract(string_to_match, strings,
limit=10, scorer=fuzzywuzzy.fuzz.token_sort_ratio)
# coger solo los que superan el límite
close_matches = [matches[0] for matches in matches if matches[1] >= min_ratio]
# coger las filas que encajan en nuestra tabla
rows_with_matches = df[column].isin(close_matches)
# reemplace todas las filas con coincidencias cercanas con las coincidencias de entrada
df.loc[rows_with_matches, column] = string_to_match
# avisar cuando acaba la función
print("All done!")
replace_matches_in_column(df=professors, column='Country', string_to_match="south korea")
countries = professors['Country'].unique()
Ventajas:
- Mejora del rendimiento en las predicciones
- Disminuye necesidad computacional y de datos
- Mejora la interpretabilidad de los resultados
Primero crear una métrica que mida la utilidad de cada característica con el objetivo, para luego escoger un conjunto menor con las características mas útiles. Para ello podemos usar la métrica Información mutua que encuentra relaciones de cualquier tipo entre variables, no sólo lineales como el coeficiente de correlación. Mide el grado que una variable reduce la incertidumbre sobre el objetivo.
from sklearn.feature_selection import mutual_info_regression
def make_mi_scores(X, y, discrete_features):
mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
mi_scores = make_mi_scores(X, y, discrete_features)
def plot_mi_scores(scores):
scores = scores.sort_values(ascending=True)
width = np.arange(len(scores))
ticks = list(scores.index)
plt.barh(width, scores)
plt.yticks(width, ticks)
plt.title("Mutual Information Scores")
plt.figure(dpi=100, figsize=(8, 5))
plot_mi_scores(mi_scores)
Es importante:
- estudiar bien:
- las características que tenemos
- el dominio de conocimiento del problema
- trabajos previos
- visualizar los datos
Observaciones:
- Los modelos lineales sólo aprenden sumas y diferencias de forma natural, pero no pueden aprender nada más complejo.
- Los modelos no suelen aprender ratios. Si se usan mejora el rendimiento.
- Modelos lineales y redes neuronales -> normalizar primero
- Los conteos son especialmente útiles en los árboles de decisión
Ratios entre variables y totales Cambio de rango y de forma: normalización
roadway_features = ["Amenity", "Bump", "Crossing", "GiveWay",
"Junction", "NoExit", "Railway", "Roundabout", "Station", "Stop",
"TrafficCalming", "TrafficSignal"]
# se crea una nueva variable con el conteo
accidents["RoadwayFeatures"] = accidents[roadway_features].sum(axis=1)
# se muestran los 10 primeros casos
accidents[roadway_features + ["RoadwayFeatures"]].head(10)
components = [ "Cement", "BlastFurnaceSlag", "FlyAsh", "Water",
"Superplasticizer", "CoarseAggregate", "FineAggregate"]
# se crea una nueva variable con el conteo cuando es mayor que 0 (gt(0))
concrete["Components"] = concrete[components].gt(0).sum(axis=1)
# se muestran los 10 primeros casos
concrete[components + ["Components"]].head(10)
customer[["Type", "Level"]] = ( # Crear dos nueva variables
customer["ColumnaA"] # de la variable ColumnaA
.str #
.split(" ", expand=True) # separando por " "
# y expandiendo en columna separadas
)
datos["variable A+B"] = datos["variable A"] + "_" + datos["variable B"]
customer["AverageIncome"] = (
customer.groupby("State") # por cada 'State'
["Income"] # seleccionar 'Income'
.transform("mean") # y calcula la media (max, min, median, var, std, and count)
)
customer[["State", "Income", "AverageIncome"]].head(10)
customer["StateFreq"] = ( # para calcular la frecuencia
customer.groupby("State")
["State"]
.transform("count")
/ customer.State.count()
)
customer[["State", "StateFreq"]].head(10)
Es un algoritmo de aprendizaje no supervisado (datos no etiquetados).
Herramienta para encontrar características en los datos.
Apicado a:
- una característica de valores reales -> discretización
- varias características de valores reales -> cuantización vectorial
El resultado es una variable categórica. Mide la similitud en base a la distancia euclídea. Se colocan k centroides creando agrupaciones en cada uno.
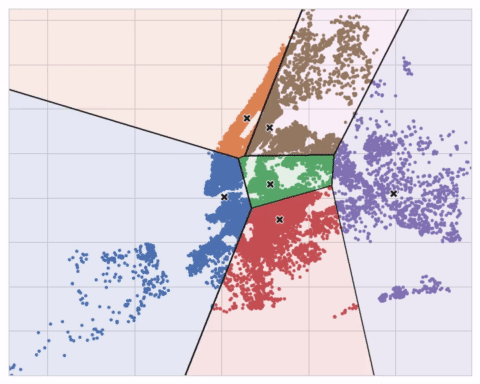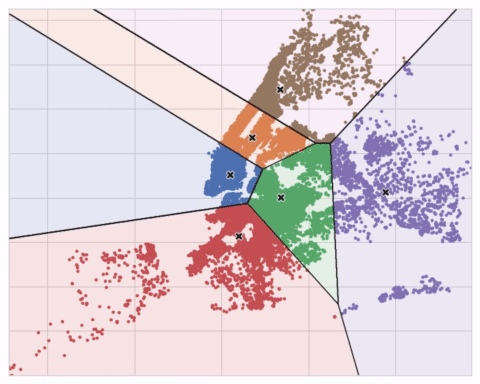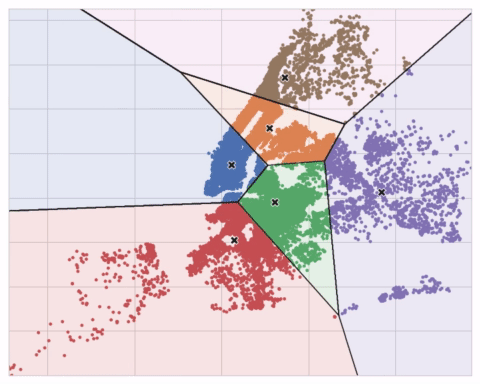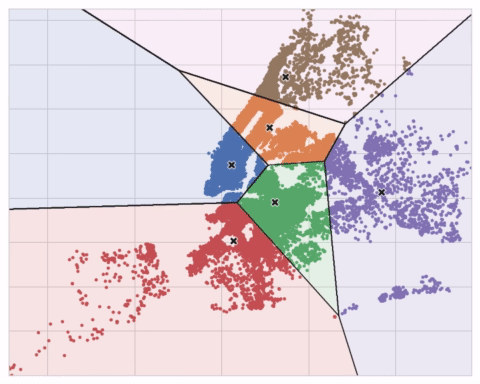
from sklearn.cluster import KMeans
X = df.copy()
y = X.pop("SalePrice")
features = ['LotArea', 'TotalBsmtSF', 'FirstFlrSF', 'SecondFlrSF','GrLivArea']
# Standardize
X_scaled = X.loc[:,features]
X_scaled = (X_scaled - X_scaled.mean(axis=0)) / X_scaled.std(axis=0)
# Fit the KMeans model to X_scaled and create the cluster labels
kmeans = KMeans(n_clusters=10,random_state=0,n_init=10)
X["Cluster"] = kmeans.fit_predict(X_scaled)
sns.relplot(
x="Longitude", y="Latitude", hue="Cluster", data=X, height=6,
);
X["MedHouseVal"] = df["MedHouseVal"]
sns.catplot(x="MedHouseVal", y="Cluster", data=X, kind="boxen", height=6);
Herramienta para encontrar relacciones en los datos y características más útiles.
Normalizar los datos antes de usar PCA.
PCA nos dice la cantidad de variación de cada componente.
Modos de usarlo:
- como técnica descriptiva
- usando los componentes como características del modelo.
Cuando usarlo:
- reducción de dimensionalidad
- detección de anomalias
- reducción de ruido
- reduccir correlación
from sklearn.decomposition import PCA
# Estandarizar
X_scaled = (X - X.mean(axis=0)) / X.std(axis=0)
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# Convertir a tabla
component_names = [f"PC{i+1}" for i in range(X_pca.shape[1])]
X_pca = pd.DataFrame(X_pca, columns=component_names)
X_pca.head()
loadings = pd.DataFrame(
pca.components_.T, # transpose the matrix of loadings
columns=component_names, # so the columns are the principal components
index=X.columns, # and the rows are the original features
)
loadings
plot_variance(pca);# Look at explained variance
Codificación por media (puede ser codificación por probabidad,impacto...)
autos["make_encoded"] = autos.groupby("make")["price"].transform("mean")
autos[["make", "price", "make_encoded"]].head(10)
Suavizado
Cuando usarlo:
- Caracterítica con muchas categorias
- Caracterítica motivada por el dominio:cuando se sospecha la importancia a pesar de tener una métrica pobre
from category_encoders import MEstimateEncoder
# Create the encoder instance. Choose m to control noise.
encoder = MEstimateEncoder(cols=["Zipcode"], m=5.0)
# Fit the encoder on the encoding split.
encoder.fit(X_encode, y_encode)
# Encode the Zipcode column to create the final training data
X_train = encoder.transform(X_pretrain)
poly = preprocessing.PolynomialFeatures(degree=3, interaction_only=True, include_bias=False)
train_poly = poly.fit_transform(df[numerical_cols])
test_poly = poly.fit_transform(df_test[numerical_cols])
df_poly = pd.DataFrame(train_poly, columns= [f"poly_{i}" for i in range(train_poly.shape[1])])
df_test_poly = pd.DataFrame(test_poly, columns= [f"poly_{i}" for i in range(test_poly.shape[1])])
quantile_list=[0,0.25,0.5,0.75,1.0]
quantile=df['cont0'].quantile(quantile_list)
quantile
quantile_labels = ['0-25Q', '25-50Q', '50-75Q', '75-100Q']
df['cont0_quantile_range'] = pd.qcut(
df['cont0'],
q=quantile_list)
df['cont0_quantile_label'] = pd.qcut(
df['cont0'],
q=quantile_list,
labels=quantile_labels)
X = X_full.select_dtypes(exclude=['object']) # To keep things simple, we'll use only numerical predictors
X_test = X_test_full.select_dtypes(exclude=['object'])
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 0)
from sklearn.tree import DecisionTreeRegressor # RandomForestRegressor
modelo = DecisionTreeRegressor(random_state=1) # escogemos el modelo Árbol de decisión
from xgboost import XGBRegressor # XGBoost
modelo = XGBRegressor()
modelo.fit(train_X, train_y) # se entrena el modelo
val_predicciones = modelo.predict(val_X) # se hace predicción
mean_absolute_error(val_y, val_predicciones) # se evalua el modelo
final_X_test = pd.DataFrame(final_imputer.transform(X_test)) # usar total de datos transformados
# Sacar las predicciones con los datos para test
preds_test = model.predict(final_X_test)
# Guardar datos a archivo
output = pd.DataFrame({'Id': X_test.index,
'SalePrice': preds_test})
output.to_csv('submission.csv', index=False)
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
# Preprocesamiento de datos numéricos
numerical_transformer = SimpleImputer(strategy='constant')
# Preprocesamiento de datos categóricos
categorical_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(handle_unknown='ignore'))
])
# Paquete de prepocesado
preprocessor = ColumnTransformer(
transformers=[
('num', numerical_transformer, numerical_cols),
('cat', categorical_transformer, categorical_cols)
])
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=100, random_state=0)
from sklearn.metrics import mean_absolute_error
# Agrupar código de preprocesamiento y modelado en una canalización
my_pipeline = Pipeline(steps=[('preprocessor', preprocessor),
('model', model)
])
# Procesamiento previo de datos de entrenamiento, modelo de ajuste
my_pipeline.fit(X_train, y_train)
# Procesamiento previo de datos de validación, obtención de predicciones
preds = my_pipeline.predict(X_valid)
# Evaluar el modelo
score = mean_absolute_error(y_valid, preds)
print('MAE:', score)
Validación cruzada (Cross-Validation)
Divide los datos en subconjuntos, realiza el entrenamiento y validación alternando los subconjuntos y calcula la media al final. Para conjuntos de datos grandes es posible que no sea necesario. Si Cross-validation da resultados similares en cada subconjunto no es necesario hacerlo.
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
my_pipeline = Pipeline(steps=[('preprocessor', SimpleImputer()),
('model', RandomForestRegressor(n_estimators=50,
random_state=0))
])
# Multiply by -1 since sklearn calculates *negative* MAE
scores = -1 * cross_val_score(my_pipeline, X, y,
cv=5,
scoring='neg_mean_absolute_error')
print("MAE scores:\n", scores)
from xgboost import XGBRegressor
from sklearn.metrics import mean_absolute_error
my_model = XGBRegressor()
my_model.fit(X_train, y_train)
predictions = my_model.predict(X_valid)
print("Mean Absolute Error: " + str(mean_absolute_error(predictions, y_valid)))
n_estimators = nº ciclos = nº modelos a añadir. Suele estar entre 100-1000 (depende mucho del ratio de aprendizaje).
- muy bajo -> underfitting
- muy alto -> overfitting
early_stopping_rounds encuentra automáticamente el valor óptimo de 'n_estimators'. Para el entrenamiento cuando el valor de validación deja de mejorar. Valor adecuado=5, para cuando lleva 5 ciclos empeorando la validación.
learning_rate = ratio de aprendizaje. Por defecto 0.1.
Por lo general, es mejor nº alto de 'n_estimators' y bajo de 'learning_rate'
n_jobs = para ejecución en paralelo de grandes conjuntos de datos = nº nucleos del ordenador
my_model = XGBRegressor(n_estimators=1000, learning_rate=0.05, n_jobs=4)
my_model.fit(X_train, y_train,
early_stopping_rounds=5,
eval_set=[(X_valid, y_valid)],
verbose=False)
Ocurre cuando el conjunto de datos tiene información de la variable de destino. Produce alta precisión en el entrenamiento, pero muy baja en la predicciones reales.
Tipos:
- target leakage: cuando se incluyen datos que tienen información posterior a lo que se desea predecir
- train-test contamination: ocurre cuando se mezclan los datos de entrenamiento y los de validación a la hora de entrenar el modelo.