1.2- NLP: Analisis del Sentimiento con Naïve Bayes
Procesamiento del lenguaje natural con Clasificación y Espacios Vectoriales
- Teorema de Bayes
- Método Naive Bayes (Bayes ingenuo)
- Suavizado Laplaciano (Laplacian Smoothing)
- Logaritmo de la probabilidad (Log Likelihood)
- Visualizando Naive Bayes
- Entrenando naïve Bayes
- Probar el modelo
- Errores que podrían causar que clasifiques mal un ejemplo o un tweet:
Teorema de Bayes
Calcula la probabilidad de que ocurra un evento A aleatorio en el caso de que ha ocurrido otro B. +info

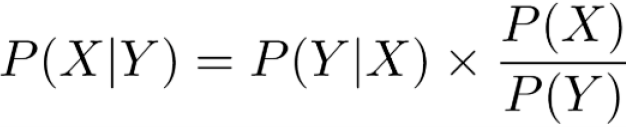
Aplicaciones:
- Identificación del autor
- Filtrado de spam
- Recuperación de información
- Desambiguación de palabras
Naïve Bayes toma una suposición de independencia: si tuviera que completar la oración "Siempre hace frío y nieve en __", este modelo ingenuo asignará el mismo peso a las palabras "primavera, verano, otoño, invierno".



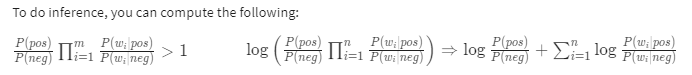
-> log prior + log likelihood
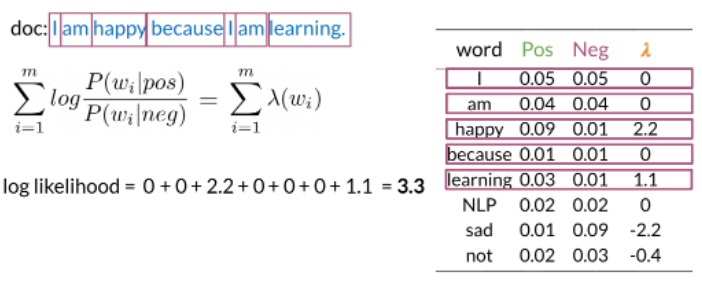
import numpy as np # Library for linear algebra and math utils
import pandas as pd # Dataframe library
import matplotlib.pyplot as plt # Library for plots
data = pd.read_csv('./data/bayes_features.csv'); # Load the data from the csv file
data.head(5) # Print the first 5 tweets features. Each row represents a tweet
fig, ax = plt.subplots(figsize = (8, 8))
colors = ['red', 'green'] # Define a color palete
sentiments = ['negative', 'positive']
index = data.index
# Color base on sentiment
for sentiment in data.sentiment.unique():
ix = index[data.sentiment == sentiment]
ax.scatter(data.iloc[ix].positive, data.iloc[ix].negative, c=colors[int(sentiment)], s=0.1, marker='*', label=sentiments[int(sentiment)])
# Custom limits for this chart
plt.xlim(-200,40)
plt.ylim(-200,40)
plt.xlabel("Positive") # x-axis label
plt.ylabel("Negative") # y-axis label
data_pos = data[data.sentiment == 1] # Filter only the positive samples
data_neg = data[data.sentiment == 0] # Filter only the negative samples
ax.legend(loc='lower right')
plt.show()
In the next cell, we will modify the features of the samples with positive sentiment (1), in a way that the two distributions overlap. In this case, the Naïve Bayes method will produce a lower accuracy than with the original data.
data2 = data.copy() # Copy the whole data frame
# The following 2 lines only modify the entries in the data frame where sentiment == 1
data2.negative[data.sentiment == 1] = data2.negative * 1.5 + 50 # Modify the negative attribute
data2.positive[data.sentiment == 1] = data2.positive / 1.5 - 50 # Modify the positive attribute
fig, ax = plt.subplots(figsize = (8, 8))
colors = ['red', 'green'] # Define a color palete
sentiments = ['negative', 'positive']
index = data2.index
# Color base on sentiment
for sentiment in data2.sentiment.unique():
ix = index[data2.sentiment == sentiment]
ax.scatter(data2.iloc[ix].positive, data2.iloc[ix].negative, c=colors[int(sentiment)], s=0.1, marker='*', label=sentiments[int(sentiment)])
#ax.scatter(data2.positive, data2.negative, c=[colors[int(k)] for k in data2.sentiment], s = 0.1, marker='*') # Plot a dot for tweet
# Custom limits for this chart
plt.xlim(-200,40)
plt.ylim(-200,40)
plt.xlabel("Positive") # x-axis label
plt.ylabel("Negative") # y-axis label
data_pos = data2[data2.sentiment == 1] # Filter only the positive samples
data_neg = data[data2.sentiment == 0] # Filter only the negative samples
ax.legend(loc='lower right')
plt.show()
Entrenando naïve Bayes
Pasos:
- Obtener un conjunto de datos con tweets positivos y negativos
-
Preprocesar los tweets: procesar_tweet(tweet) ➞ [w1, w2, w3, ...]:
- Minúsculas
- Eliminar puntuación, URL, nombres
- Eliminar palabras vacías
- Derivación
- Tokenizar oraciones
-
Calcular frecuencia (w, clase)
- Obtener P(w|pos),P(w|neg)
- Obtener λ(w)
- Calcular logprior = log(P(pos) / P(neg)), el número de documentos positivos y negativos
import pdb
from nltk.corpus import stopwords, twitter_samples
import numpy as np
import pandas as pd
import nltk
import string
from nltk.tokenize import TweetTokenizer
from os import getcwd
import re
import string
from nltk.stem import PorterStemmer
nltk.download('twitter_samples')
nltk.download('stopwords')
filePath = f"{getcwd()}/../tmp2/"
nltk.data.path.append(filePath)
def process_tweet(tweet):
'''
Input:
tweet: a string containing a tweet
Output:
tweets_clean: a list of words containing the processed tweet
'''
stemmer = PorterStemmer()
stopwords_english = stopwords.words('english')
# remove stock market tickers like $GE
tweet = re.sub(r'\$\w*', '', tweet)
# remove old style retweet text "RT"
tweet = re.sub(r'^RT[\s]+', '', tweet)
# remove hyperlinks
tweet = re.sub(r'https?:\/\/.*[\r\n]*', '', tweet)
# remove hashtags
# only removing the hash # sign from the word
tweet = re.sub(r'#', '', tweet)
# tokenize tweets
tokenizer = TweetTokenizer(preserve_case=False, strip_handles=True,
reduce_len=True)
tweet_tokens = tokenizer.tokenize(tweet)
tweets_clean = []
for word in tweet_tokens:
if (word not in stopwords_english and # remove stopwords
word not in string.punctuation): # remove punctuation
# tweets_clean.append(word)
stem_word = stemmer.stem(word) # stemming word
tweets_clean.append(stem_word)
return tweets_clean
def lookup(freqs, word, label):
'''
Input:
freqs: a dictionary with the frequency of each pair (or tuple)
word: the word to look up
label: the label corresponding to the word
Output:
n: the number of times the word with its corresponding label appears.
'''
n = 0 # freqs.get((word, label), 0)
pair = (word, label)
if (pair in freqs):
n = freqs[pair]
return n
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
# split the data into two pieces, one for training and one for testing (validation set)
test_pos = all_positive_tweets[4000:]
train_pos = all_positive_tweets[:4000]
test_neg = all_negative_tweets[4000:]
train_neg = all_negative_tweets[:4000]
train_x = train_pos + train_neg
test_x = test_pos + test_neg
# avoid assumptions about the length of all_positive_tweets
train_y = np.append(np.ones(len(train_pos)), np.zeros(len(train_neg)))
test_y = np.append(np.ones(len(test_pos)), np.zeros(len(test_neg)))
custom_tweet = "RT @Twitter @chapagain Hello There! Have a great day. :) #good #morning http://chapagain.com.np"
# print cleaned tweet
print(process_tweet(custom_tweet))
def count_tweets(result, tweets, ys):
'''
Input:
result: a dictionary that will be used to map each pair to its frequency
tweets: a list of tweets
ys: a list corresponding to the sentiment of each tweet (either 0 or 1)
Output:
result: a dictionary mapping each pair to its frequency
'''
for y, tweet in zip(ys, tweets):
for word in process_tweet(tweet):
# define the key, which is the word and label tuple
pair = (word,y)
# if the key exists in the dictionary, increment the count
if pair in result:
result[pair] += 1
# else, if the key is new, add it to the dictionary and set the count to 1
else:
result[pair] = 1
return result
result = {}
tweets = ['i am happy', 'i am tricked', 'i am sad', 'i am tired', 'i am tired']
ys = [1, 0, 0, 0, 0]
count_tweets(result, tweets, ys)
freqs = count_tweets({}, train_x, train_y)
def train_naive_bayes(freqs, train_x, train_y):
'''
Input:
freqs: dictionary from (word, label) to how often the word appears
train_x: a list of tweets
train_y: a list of labels correponding to the tweets (0,1)
Output:
logprior: the log prior. (equation 3 above)
loglikelihood: the log likelihood of you Naive bayes equation. (equation 6 above)
'''
loglikelihood = {}
logprior = 0
# calculate V, the number of unique words in the vocabulary
vocab = set([tupla[0] for tupla in freqs])
V = len(vocab)
# calculate N_pos, N_neg, V_pos, V_neg
N_pos = N_neg = 0
for pair in freqs.keys():
# if the label is positive (greater than zero)
if pair[1] > 0:
# Increment the number of positive words by the count for this (word, label) pair
N_pos += freqs[pair]
# else, the label is negative
else:
# increment the number of negative words by the count for this (word,label) pair
N_neg += freqs[pair]
# Calculate D, the number of documents
D = len(train_y)
# Calculate D_pos, the number of positive documents
D_pos = sum(train_y)
# Calculate D_neg, the number of negative documents
D_neg = D-D_pos
# Calculate logprior
logprior = np.log(D_pos)-np.log(D_neg)
# For each word in the vocabulary...
for word in vocab:
# get the positive and negative frequency of the word
if (word,1) in freqs:
freq_pos = freqs[word,1]
else:
freq_pos = 0
if (word,0) in freqs:
freq_neg = freqs[word,0]
else:
freq_neg = 0
# calculate the probability that each word is positive, and negative
p_w_pos = (freq_pos+1)/(N_pos+V)
p_w_neg = (freq_neg+1)/(N_neg+V)
# calculate the log likelihood of the word
loglikelihood[word] = np.log(p_w_pos)- np.log(p_w_neg)
### END CODE HERE ###
return logprior, loglikelihood
logprior, loglikelihood = train_naive_bayes(freqs, train_x, train_y)
print(logprior)
print(len(loglikelihood))
def naive_bayes_predict(tweet, logprior, loglikelihood):
'''
Input:
tweet: a string
logprior: a number
loglikelihood: a dictionary of words mapping to numbers
Output:
p: the sum of all the logliklihoods of each word in the tweet (if found in the dictionary) + logprior (a number)
'''
# process the tweet to get a list of words
word_l = process_tweet(tweet)
# initialize probability to zero
p = 0
# add the logprior
p += logprior
for word in word_l:
# check if the word exists in the loglikelihood dictionary
if word in loglikelihood:
# add the log likelihood of that word to the probability
p += loglikelihood[word]
return p
my_tweet = 'She smiled.'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print('The expected output is', p)
def test_naive_bayes(test_x, test_y, logprior, loglikelihood, naive_bayes_predict=naive_bayes_predict):
"""
Input:
test_x: A list of tweets
test_y: the corresponding labels for the list of tweets
logprior: the logprior
loglikelihood: a dictionary with the loglikelihoods for each word
Output:
accuracy: (# of tweets classified correctly)/(total # of tweets)
"""
accuracy = 0 # return this properly
y_hats = []
for tweet in test_x:
# if the prediction is > 0
if naive_bayes_predict(tweet, logprior, loglikelihood) > 0:
# the predicted class is 1
y_hat_i = 1
else:
# otherwise the predicted class is 0
y_hat_i = 0
# append the predicted class to the list y_hats
y_hats.append(y_hat_i)
# error is the average of the absolute values of the differences between y_hats and test_y
error = sum(abs(y_hats-test_y))/len(test_y)
# Accuracy is 1 minus the error
accuracy = 1-error
return accuracy
print("Naive Bayes accuracy = %0.4f" %
(test_naive_bayes(test_x, test_y, logprior, loglikelihood)))
for tweet in ['I am happy', 'I am bad', 'this movie should have been great.', 'great', 'great great', 'great great great', 'great great great great']:
p = naive_bayes_predict(tweet, logprior, loglikelihood)
print(f'{tweet} -> {p:.2f}')

