1.4- NLP: Traducción automática y búsqueda de documentos
Procesamiento del lenguaje natural con Clasificación y Espacios Vectoriales
- Transformar vectores de palabras
- K-vecinos más próximos (KNN: K-nearest neighbors)
- Vecinos cercanos aproximados
- Traducción automática ingenua
- Los word embeddings para palabras en inglés y francés
- LSH (locality sensitive hashing) y búsqueda de documentos
Tip: Puedes ver este post en GitHub o ejecutarlo en Binder o Google Colab, pulsa el icono.
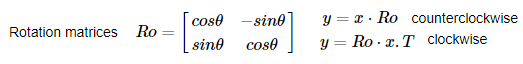
Hashing
- hash_function = toma datos de tamaños arbitrarios y los asigna a un valor fijo.
- No hace falta compararlo con todos los ejemplos, simplemente con los valores en el mismo hash_bucket (cubo hash) al que se ha aplicado a la entrada el hash.
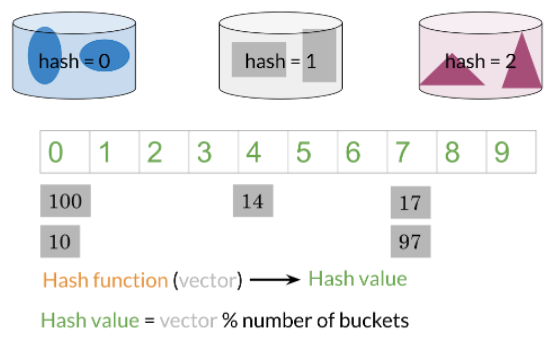

def basic_hash_table(value_l, n_buckets):
def hash_function(value, n_buckets):
return int(value) % n_buckets
hash_table = {i:[] for i in range(n_buckets)} # Initialize all the buckets in the hash table as empty lists
for value in value_l:
hash_value = hash_function(value,n_buckets) # Get the hash key for the given value
hash_table[hash_value].append(value) # Add the element to the corresponding bucket
return hash_table
value_l = [100, 10, 14, 17, 97] # Set of values to hash
hash_table_example = basic_hash_table(value_l, n_buckets=10)
pp.pprint(hash_table_example)

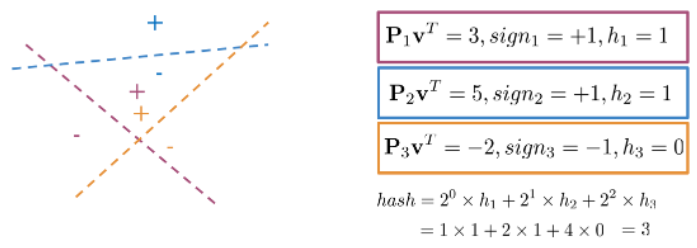
import numpy as np # library for array and matrix manipulation
import pandas as pd
import pprint # utilities for console printing
import matplotlib.pyplot as plt # visualization library
pp = pprint.PrettyPrinter(indent=4) # Instantiate a pretty printer
import pdb
import pickle
import string
import time
#import gensim
import nltk
import scipy
import sklearn
import re
import string
#from gensim.models import KeyedVectors
from nltk.corpus import stopwords, twitter_samples
from nltk.tokenize import TweetTokenizer
from nltk.stem import PorterStemmer
from os import getcwd
filePath = f"{getcwd()}/tmp2/"
nltk.data.path.append(filePath)
def get_dict(file_name):
"""
This function returns the english to french dictionary given a file where the each column corresponds to a word.
Check out the files this function takes in your workspace.
"""
my_file = pd.read_csv(file_name, delimiter=' ')
etof = {} # the english to french dictionary to be returned
for i in range(len(my_file)):
# indexing into the rows.
en = my_file.loc[i][0]
fr = my_file.loc[i][1]
etof[en] = fr
return etof
def cosine_similarity(A, B):
'''
Input:
A: a numpy array which corresponds to a word vector
B: A numpy array which corresponds to a word vector
Output:
cos: numerical number representing the cosine similarity between A and B.
'''
# you have to set this variable to the true label.
cos = -10
dot = np.dot(A, B)
norma = np.linalg.norm(A)
normb = np.linalg.norm(B)
cos = dot / (norma * normb)
return cos
def process_tweet(tweet):
'''
Input:
tweet: a string containing a tweet
Output:
tweets_clean: a list of words containing the processed tweet
'''
stemmer = PorterStemmer()
stopwords_english = stopwords.words('english')
# remove stock market tickers like $GE
tweet = re.sub(r'\$\w*', '', tweet)
# remove old style retweet text "RT"
tweet = re.sub(r'^RT[\s]+', '', tweet)
# remove hyperlinks
tweet = re.sub(r'https?:\/\/.*[\r\n]*', '', tweet)
# remove hashtags
# only removing the hash # sign from the word
tweet = re.sub(r'#', '', tweet)
# tokenize tweets
tokenizer = TweetTokenizer(preserve_case=False, strip_handles=True,
reduce_len=True)
tweet_tokens = tokenizer.tokenize(tweet)
tweets_clean = []
for word in tweet_tokens:
if (word not in stopwords_english and # remove stopwords
word not in string.punctuation): # remove punctuation
# tweets_clean.append(word)
stem_word = stemmer.stem(word) # stemming word
tweets_clean.append(stem_word)
return tweets_clean
def plot_vectors(vectors, colors=['k', 'b', 'r', 'm', 'c'], axes=None, fname='image.svg', ax=None):
scale = 1
scale_units = 'x'
x_dir = []
y_dir = []
for i, vec in enumerate(vectors):
x_dir.append(vec[0][0])
y_dir.append(vec[0][1])
if ax == None:
fig, ax2 = plt.subplots()
else:
ax2 = ax
if axes == None:
x_axis = 2 + np.max(np.abs(x_dir))
y_axis = 2 + np.max(np.abs(y_dir))
else:
x_axis = axes[0]
y_axis = axes[1]
ax2.axis([-x_axis, x_axis, -y_axis, y_axis])
for i, vec in enumerate(vectors):
ax2.arrow(0, 0, vec[0][0], vec[0][1], head_width=0.05 * x_axis, head_length=0.05 * y_axis, fc=colors[i], ec=colors[i])
if ax == None:
plt.show()
fig.savefig(fname)
P = np.array([[1, 1.5]]) # Define a single plane. You may change the direction
# Get a new plane perpendicular to P. We use a rotation matrix
PT = np.dot([[0, 1], [-1, 0]], P.T).T
fig, ax1 = plt.subplots(figsize=(8, 8)) # Create a plot with custom size
plot_vectors([P], colors=['b'], axes=[2, 2], ax=ax1) # Plot the plane P as a vector
# Plot the plane P as a 2 vectors.
# We scale by 2 just to get the arrows outside the current box
plot_vectors([PT * 4, PT * -4], colors=['k', 'k'], axes=[4, 4], ax=ax1)
# Plot 20 random points.
for i in range(0, 20):
v1 = np.array(np.random.uniform(-4, 4, 2)) # Get a pair of random numbers between -4 and 4
side_of_plane = np.sign(np.dot(P, v1.T)) # Get the sign of the dot product with P
# Color the points depending on the sign of the result of np.dot(P, point.T)
if side_of_plane == 1:
ax1.plot([v1[0]], [v1[1]], 'bo') # Plot a blue point
else:
ax1.plot([v1[0]], [v1[1]], 'ro') # Plot a red point
plt.show()
def side_of_plane_scalar(P, v): # scalar
dotproduct = np.dot(P, v.T) # Get the dot product P * v'
sign_of_dot_product = np.sign(dotproduct) # The sign of the elements of the dotproduct matrix
sign_of_dot_product_scalar = sign_of_dot_product.item() # The value of the first item
return sign_of_dot_product_scalar
def hash_multi_plane(P_l, v):
hash_value = 0
for i, P in enumerate(P_l):
sign = side_of_plane_scalar(P,v)
hash_i = 1 if sign >=0 else 0
hash_value += 2**i * hash_i
return hash_value
P1 = np.array([[1, 1]]) # First plane 2D
P2 = np.array([[-1, 1]]) # Second plane 2D
P3 = np.array([[-1, -1]]) # Third plane 2D
P_l = [P1, P2, P3] # List of arrays. It is the multi plane
# Vector to search
v = np.array([[2,2]])
hash_multi_plane(P_l, v) # Find the number of the plane that containes this value
def side_of_plane_matrix(P, v):
dotproduct = np.dot(P, v.T)
sign_of_dot_product = np.sign(dotproduct) # Get a boolean value telling if the value in the cell is positive or negative
return sign_of_dot_product
np.random.seed(1)
num_dimensions = 2 # is 300 in assignment
num_planes = 3 # is 10 in assignment
random_planes_matrix = np.random.normal(
size=(num_planes,
num_dimensions))
print(random_planes_matrix)
sides_l = side_of_plane_matrix(random_planes_matrix, v)
sides_l
en_embeddings_subset = pickle.load(open("./data/en_embeddings.p", "rb"))
fr_embeddings_subset = pickle.load(open("./data/fr_embeddings.p", "rb"))
en_fr_train = get_dict('./data/en-fr.train.txt')
print('The length of the English to French training dictionary is', len(en_fr_train))
en_fr_test = get_dict('./data/en-fr.test.txt')
print('The length of the English to French test dictionary is', len(en_fr_test))
def get_matrices(en_fr, french_vecs, english_vecs):
"""
Input:
en_fr: English to French dictionary
french_vecs: French words to their corresponding word embeddings.
english_vecs: English words to their corresponding word embeddings.
Output:
X: a matrix where the columns are the English embeddings.
Y: a matrix where the columns correspong to the French embeddings.
R: the projection matrix that minimizes the F norm ||X R -Y||^2.
"""
# X_l and Y_l are lists of the english and french word embeddings
X_l = list()
Y_l = list()
# get the english words (the keys in the dictionary) and store in a set()
english_set = set(english_vecs.keys())
# get the french words (keys in the dictionary) and store in a set()
french_set = set(french_vecs.keys())
# store the french words that are part of the english-french dictionary (these are the values of the dictionary)
french_words = set(en_fr.values())
# loop through all english, french word pairs in the english french dictionary
for en_word, fr_word in en_fr.items():
# check that the french word has an embedding and that the english word has an embedding
if fr_word in french_set and en_word in english_set:
# get the english embedding
en_vec = english_vecs[en_word]
# get the french embedding
fr_vec = french_vecs[fr_word]
# add the english embedding to the list
X_l.append(en_vec)
# add the french embedding to the list
Y_l.append(fr_vec)
# stack the vectors of X_l into a matrix X
X = np.array(X_l)
# stack the vectors of Y_l into a matrix Y
Y = np.array(Y_l)
return X, Y
X_train, Y_train = get_matrices(
en_fr_train, fr_embeddings_subset, en_embeddings_subset)
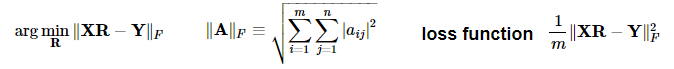
def compute_loss(X, Y, R):
'''
Inputs:
X: a matrix of dimension (m,n) where the columns are the English embeddings.
Y: a matrix of dimension (m,n) where the columns correspong to the French embeddings.
R: a matrix of dimension (n,n) - transformation matrix from English to French vector space embeddings.
Outputs:
L: a matrix of dimension (m,n) - the value of the loss function for given X, Y and R.
'''
# m is the number of rows in X
m = len(X)
# diff is XR - Y
diff = np.dot(X,R)-Y
# diff_squared is the element-wise square of the difference
diff_squared = diff**2
# sum_diff_squared is the sum of the squared elements
sum_diff_squared = np.sum(diff_squared)
# loss i the sum_diff_squard divided by the number of examples (m)
loss = sum_diff_squared / m
return loss
np.random.seed(123)
m = 10
n = 5
X = np.random.rand(m, n)
Y = np.random.rand(m, n) * .1
R = np.random.rand(n, n)
print(f"Expected loss for an experiment with random matrices: {compute_loss(X, Y, R):.4f}" )
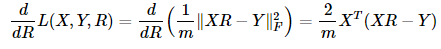
def compute_gradient(X, Y, R):
'''
Inputs:
X: a matrix of dimension (m,n) where the columns are the English embeddings.
Y: a matrix of dimension (m,n) where the columns correspong to the French embeddings.
R: a matrix of dimension (n,n) - transformation matrix from English to French vector space embeddings.
Outputs:
g: a scalar value - gradient of the loss function L for given X, Y and R.
'''
# m is the number of rows in X
m = len(X)
# gradient is X^T(XR - Y) * 2/m
gradient = np.dot(X.T,(np.dot(X,R)-Y))*2/m
return gradient
np.random.seed(123)
m = 10
n = 5
X = np.random.rand(m, n)
Y = np.random.rand(m, n) * .1
R = np.random.rand(n, n)
gradient = compute_gradient(X, Y, R)
print(f"First row of the gradient matrix: {gradient[0]}")
def align_embeddings(X, Y, train_steps=100, learning_rate=0.0003, verbose=True, compute_loss=compute_loss, compute_gradient=compute_gradient):
'''
Inputs:
X: a matrix of dimension (m,n) where the columns are the English embeddings.
Y: a matrix of dimension (m,n) where the columns correspong to the French embeddings.
train_steps: positive int - describes how many steps will gradient descent algorithm do.
learning_rate: positive float - describes how big steps will gradient descent algorithm do.
Outputs:
R: a matrix of dimension (n,n) - the projection matrix that minimizes the F norm ||X R -Y||^2
'''
np.random.seed(129)
# the number of columns in X is the number of dimensions for a word vector (e.g. 300)
# R is a square matrix with length equal to the number of dimensions in th word embedding
R = np.random.rand(X.shape[1], X.shape[1])
for i in range(train_steps):
if verbose and i % 25 == 0:
print(f"loss at iteration {i} is: {compute_loss(X, Y, R):.4f}")
# use the function that you defined to compute the gradient
gradient = compute_gradient(X, Y, R)
# update R by subtracting the learning rate times gradient
R -= learning_rate * gradient
return R
np.random.seed(129)
m = 10
n = 5
X = np.random.rand(m, n)
Y = np.random.rand(m, n) * .1
R = align_embeddings(X, Y)
R_train = align_embeddings(X_train, Y_train, train_steps=400, learning_rate=0.8)
Buscando la traducción del embedding
Dado que estamos aproximando la función de traducción de embeddings de inglés a francés mediante una matriz de transformación lineal R , la mayoría de las veces no obtendremos el embedding exacto de una palabra en francés.
Aquí es donde k-NN se vuelve realmente útil. Al usar 1-NN con eR como entrada, podemos buscar un embedding f (como una fila) en la matriz Y que sea la más cercana al vector transformado eR
def nearest_neighbor(v, candidates, k=1, cosine_similarity=cosine_similarity):
"""
Input:
- v, the vector you are going find the nearest neighbor for
- candidates: a set of vectors where we will find the neighbors
- k: top k nearest neighbors to find
Output:
- k_idx: the indices of the top k closest vectors in sorted form
"""
similarity_l = []
# for each candidate vector...
for row in candidates:
# get the cosine similarity
cos_similarity = np.dot(v,row)/(np.linalg.norm(v)*np.linalg.norm(row))
# append the similarity to the list
similarity_l.append(cos_similarity)
# sort the similarity list and get the indices of the sorted list
sorted_ids = np.argsort(similarity_l)
# Reverse the order of the sorted_ids array
sorted_ids = sorted_ids[::-1]
# get the indices of the k most similar candidate vectors
k_idx = sorted_ids[:k]
return k_idx
v = np.array([1, 0, 1])
candidates = np.array([[1, 0, 5], [-2, 5, 3], [2, 0, 1], [6, -9, 5], [9, 9, 9]])
print(candidates[nearest_neighbor(v, candidates, 3)])
def test_vocabulary(X, Y, R, nearest_neighbor=nearest_neighbor):
'''
Input:
X: a matrix where the columns are the English embeddings.
Y: a matrix where the columns correspong to the French embeddings.
R: the transform matrix which translates word embeddings from
English to French word vector space.
Output:
accuracy: for the English to French capitals
'''
# The prediction is X times R
pred = np.dot(X,R)
# initialize the number correct to zero
num_correct = 0
# loop through each row in pred (each transformed embedding)
for i in range(len(pred)):
# get the index of the nearest neighbor of pred at row 'i'; also pass in the candidates in Y
pred_idx = nearest_neighbor(pred[i], Y, k=1, cosine_similarity=cosine_similarity)
# if the index of the nearest neighbor equals the row of i... \
if pred_idx == i:
# increment the number correct by 1.
num_correct += 1
# accuracy is the number correct divided by the number of rows in 'pred' (also number of rows in X)
accuracy = num_correct / len(pred)
return accuracy
X_val, Y_val = get_matrices(en_fr_test, fr_embeddings_subset, en_embeddings_subset)
acc = test_vocabulary(X_val, Y_val, R_train) # this might take a minute or two
print(f"accuracy on test set is {acc:.3f}")
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
all_tweets = all_positive_tweets + all_negative_tweets
Obtener los iembeddings de documentos
Modelos de documento de bolsa de palabras (BOW): los documentos de texto son secuencias de palabras.
- El orden de las palabras marca la diferencia. Por ejemplo, las oraciones "La tarta de manzana es mejor que la pizza de pepperoni". y "La pizza de pepperoni es mejor que la tarta de manzana" tienen significados opuestos debido al orden de las palabras.
- Sin embargo, para algunas aplicaciones, ignorar el orden de las palabras puede permitirnos entrenar un modelo eficiente y efectivo. Este enfoque se denomina modelo de documento de bolsa de palabras. Embeddings de documentos
- Los embeddings de documentos se crea sumando los embeddings de todas las palabras en el documento.
- Si no conocemos el embeddings de alguna palabra, podemos ignorar esa palabra.
def get_document_embedding(tweet, en_embeddings, process_tweet=process_tweet):
'''
Input:
- tweet: a string
- en_embeddings: a dictionary of word embeddings
Output:
- doc_embedding: sum of all word embeddings in the tweet
'''
doc_embedding = np.zeros(300)
# process the document into a list of words (process the tweet)
processed_doc = process_tweet(tweet)
for word in processed_doc:
# add the word embedding to the running total for the document embedding
if word in en_embeddings.keys():
doc_embedding += en_embeddings[word]
return doc_embedding
custom_tweet = "RT @Twitter @chapagain Hello There! Have a great day. :) #good #morning http://chapagain.com.np"
tweet_embedding = get_document_embedding(custom_tweet, en_embeddings_subset)
tweet_embedding[-5:]
def get_document_vecs(all_docs, en_embeddings, get_document_embedding=get_document_embedding):
'''
Input:
- all_docs: list of strings - all tweets in our dataset.
- en_embeddings: dictionary with words as the keys and their embeddings as the values.
Output:
- document_vec_matrix: matrix of tweet embeddings.
- ind2Doc_dict: dictionary with indices of tweets in vecs as keys and their embeddings as the values.
'''
# the dictionary's key is an index (integer) that identifies a specific tweet
# the value is the document embedding for that document
ind2Doc_dict = {}
# this is list that will store the document vectors
document_vec_l = []
for i, doc in enumerate(all_docs):
# get the document embedding of the tweet
doc_embedding = get_document_embedding(doc, en_embeddings, process_tweet=process_tweet)
# save the document embedding into the ind2Tweet dictionary at index i
ind2Doc_dict[i] = doc_embedding
# append the document embedding to the list of document vectors
document_vec_l.append(doc_embedding)
# convert the list of document vectors into a 2D array (each row is a document vector)
document_vec_matrix = np.vstack(document_vec_l)
return document_vec_matrix, ind2Doc_dict
document_vecs, ind2Tweet = get_document_vecs(all_tweets, en_embeddings_subset)
print(f"length of dictionary {len(ind2Tweet)}")
print(f"shape of document_vecs {document_vecs.shape}")
my_tweet = 'i am sad'
process_tweet(my_tweet)
tweet_embedding = get_document_embedding(my_tweet, en_embeddings_subset)
# this implementation is vectorized...
idx = np.argmax(cosine_similarity(document_vecs, tweet_embedding))
print(all_tweets[idx])
N_VECS = len(all_tweets) # This many vectors.
N_DIMS = len(ind2Tweet[1]) # Vector dimensionality.
print(f"Number of vectors is {N_VECS} and each has {N_DIMS} dimensions.")
# The number of planes. We use log2(256) to have ~16 vectors/bucket.
N_PLANES = 10
# Number of times to repeat the hashing to improve the search.
N_UNIVERSES = 25
Elegir el número de planos
- Cada plano divide el espacio en 2 partes.
- Entonces n planos dividen el espacio en 2n cubos de hash.
- Queremos organizar 10,000 vectores de documentos en cubos para que cada cubo tenga alrededor de 16 vectores.
- Para eso necesitamos 10000/16=625 cubos.
- Nos interesa n , número de planos, por lo que 2n=625 . Ahora, podemos calcular n=log2 625=9.29≈10 .
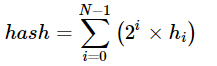
np.random.seed(0)
planes_l = [np.random.normal(size=(N_DIMS, N_PLANES))
for _ in range(N_UNIVERSES)]
def hash_value_of_vector(v, planes):
"""Create a hash for a vector; hash_id says which random hash to use.
Input:
- v: vector of tweet. It's dimension is (1, N_DIMS)
- planes: matrix of dimension (N_DIMS, N_PLANES) - the set of planes that divide up the region
Output:
- res: a number which is used as a hash for your vector
"""
# for the set of planes, calculate the dot product between the vector and the matrix containing the planes
# remember that planes has shape (300, 10) The dot product will have the shape (1,10)
dot_product = np.dot(v,planes)
# get the sign of the dot product (1,10) shaped vector
sign_of_dot_product = np.sign(dot_product )
# set h to be false (eqivalent to 0 when used in operations) if the sign is negative,
# and true (equivalent to 1) if the sign is positive (1,10) shaped vector
# if the sign is 0, i.e. the vector is in the plane, consider the sign to be positive
h= sign_of_dot_product >= 1
# remove extra un-used dimensions (convert this from a 2D to a 1D array)
h = np.squeeze(h)
# initialize the hash value to 0
hash_value = 0
n_planes = len(planes[0])
for i in range(n_planes):
# increment the hash value by 2^i * h_i
hash_value += (2**i)* h[i]
# cast hash_value as an integer
hash_value = int(hash_value)
return hash_value
np.random.seed(0)
idx = 0
planes = planes_l[idx] # get one 'universe' of planes to test the function
vec = np.random.rand(1, 300)
print(f" The hash value for this vector,",
f"and the set of planes at index {idx},",
f"is {hash_value_of_vector(vec, planes)}")
def make_hash_table(vecs, planes, hash_value_of_vector=hash_value_of_vector):
"""
Input:
- vecs: list of vectors to be hashed.
- planes: the matrix of planes in a single "universe", with shape (embedding dimensions, number of planes).
Output:
- hash_table: dictionary - keys are hashes, values are lists of vectors (hash buckets)
- id_table: dictionary - keys are hashes, values are list of vectors id's
(it's used to know which tweet corresponds to the hashed vector)
"""
# number of planes is the number of columns in the planes matrix
num_of_planes = len(planes[0])
# number of buckets is 2^(number of planes)
num_buckets = 2**num_of_planes
# create the hash table as a dictionary.
# Keys are integers (0,1,2.. number of buckets)
# Values are empty lists
hash_table = {i : [] for i in range(num_buckets)}
# create the id table as a dictionary.
# Keys are integers (0,1,2... number of buckets)
# Values are empty lists
id_table = {i : [] for i in range(num_buckets)}
# for each vector in 'vecs'
for i, v in enumerate(vecs):
# calculate the hash value for the vector
h = hash_value_of_vector(v, planes)
# store the vector into hash_table at key h,
# by appending the vector v to the list at key h
hash_table[h].append(v)
# store the vector's index 'i' (each document is given a unique integer 0,1,2...)
# the key is the h, and the 'i' is appended to the list at key h
id_table[h].append(i)
return hash_table, id_table
planes = planes_l[0] # get one 'universe' of planes to test the function
tmp_hash_table, tmp_id_table = make_hash_table(document_vecs, planes)
print(f"The hash table at key 0 has {len(tmp_hash_table[0])} document vectors")
print(f"The id table at key 0 has {len(tmp_id_table[0])}")
print(f"The first 5 document indices stored at key 0 of are {tmp_id_table[0][0:5]}")
def create_hash_id_tables(n_universes):
hash_tables = []
id_tables = []
for universe_id in range(n_universes): # there are 25 hashes
print('working on hash universe #:', universe_id)
planes = planes_l[universe_id]
hash_table, id_table = make_hash_table(document_vecs, planes)
hash_tables.append(hash_table)
id_tables.append(id_table)
return hash_tables, id_tables
hash_tables, id_tables = create_hash_id_tables(N_UNIVERSES)
def approximate_knn(doc_id, v, planes_l, hash_tables, id_tables, k=1, num_universes_to_use=25, hash_value_of_vector=hash_value_of_vector):
"""Search for k-NN using hashes."""
#assert num_universes_to_use <= N_UNIVERSES
vecs_to_consider_l = list() # Vectors that will be checked as possible nearest neighbor
ids_to_consider_l = list() # list of document IDs
ids_to_consider_set = set() # create a set for ids to consider, for faster checking if a document ID already exists in the set
# loop through the universes of planes
for universe_id in range(num_universes_to_use):
planes = planes_l[universe_id] # get the set of planes from the planes_l list, for this particular universe_id
hash_value = hash_value_of_vector(v, planes) # get the hash value of the vector for this set of planes
hash_table = hash_tables[universe_id] # get the hash table for this particular universe_id
document_vectors_l = hash_table[hash_value] # get the list of document vectors for this hash table, where the key is the hash_value
id_table = id_tables[universe_id] # get the id_table for this particular universe_id
new_ids_to_consider = id_table[hash_value] # get the subset of documents to consider as nearest neighbors from this id_table dictionary
if doc_id in new_ids_to_consider:
new_ids_to_consider.remove(doc_id) #-----
print(
f"removed doc_id {doc_id} of input vector from new_ids_to_search")
# loop through the subset of document vectors to consider
for i, new_id in enumerate(new_ids_to_consider):
# if the document ID is not yet in the set ids_to_consider...
if new_id not in ids_to_consider_set:
# access document_vectors_l list at index i to get the embedding
# then append it to the list of vectors to consider as possible nearest neighbors
document_vector_at_i = get_document_embedding(all_tweets[i], en_embeddings_subset, process_tweet=process_tweet) #-----
vecs_to_consider_l.append(document_vector_at_i) #-----
# append the new_id (the index for the document) to the list of ids to consider
ids_to_consider_l.append(new_id)
# also add the new_id to the set of ids to consider
# (use this to check if new_id is not already in the IDs to consider)
ids_to_consider_set.add(new_id)
# Now run k-NN on the smaller set of vecs-to-consider.
print("Fast considering %d vecs" % len(vecs_to_consider_l))
# convert the vecs to consider set to a list, then to a numpy array
vecs_to_consider_arr = np.array(vecs_to_consider_l)
# call nearest neighbors on the reduced list of candidate vectors
nearest_neighbor_idx_l = nearest_neighbor(v, vecs_to_consider_arr, k=k)
# Use the nearest neighbor index list as indices into the ids to consider
# create a list of nearest neighbors by the document ids
nearest_neighbor_ids = [ids_to_consider_l[idx]
for idx in nearest_neighbor_idx_l]
return nearest_neighbor_ids
doc_id = 5
doc_to_search = all_tweets[doc_id]
vec_to_search = document_vecs[doc_id]
nearest_neighbor_ids = approximate_knn(
doc_id, vec_to_search, planes_l, hash_tables, id_tables, k=3, num_universes_to_use=5)
print(f"Nearest neighbors for document {doc_id}")
print(f"Document contents: {doc_to_search}")
print("")
for neighbor_id in nearest_neighbor_ids:
print(f"Nearest neighbor at document id {neighbor_id}")
print(f"document contents: {all_tweets[neighbor_id]}")
