Redes neuronales
Introducción intuitiva a las redes neuronales por Carlos Santana (Dot CSV)
Fuente: Carlos Santana - Dot CSV
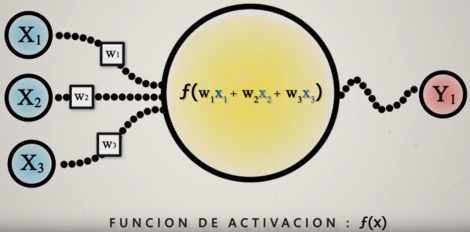
Es la unidad básica de procesamiento de una red neuronal. Tiene unos valores de entrada (x) y genera un resultado de salida (y), es decir, es una función.
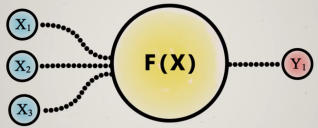
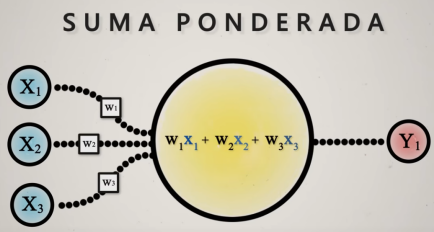
El cálculo interno es una suma ponderada, a cada valor de entrada x se le asigna un peso:
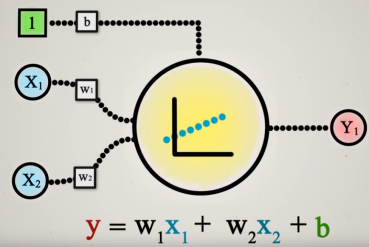
Representa un modelo de regresión lineal:
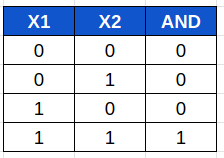
Si escogemos un ejemplo sencillo de dos variables binarias (que toman valores 0,1) x1 y x2 , podemos definir el valor de y así:

Representandolo gráficamente:
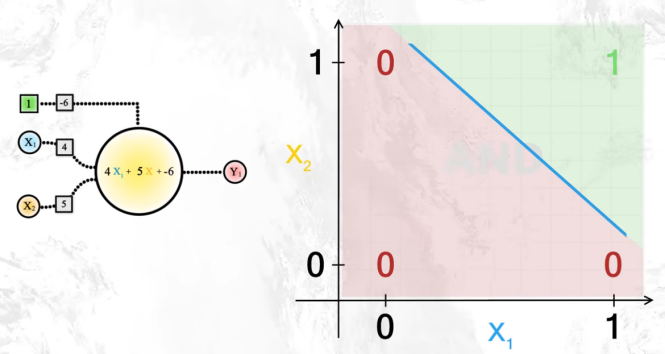
Podemos ver que hemos construido una puerta AND.
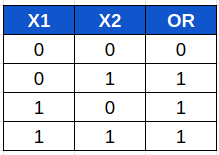
También podríamos construir una puerta OR modificando los parámetros w y b:
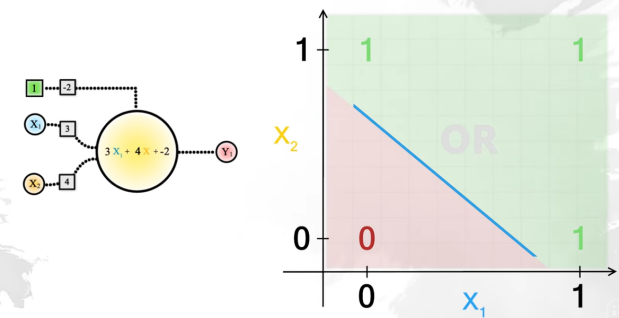
Sin embargo, una puerta XOR no se puede construir con una sola neurona. No hay una recta que separe los 0 de los 1:
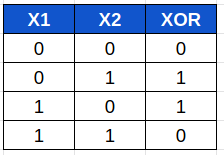
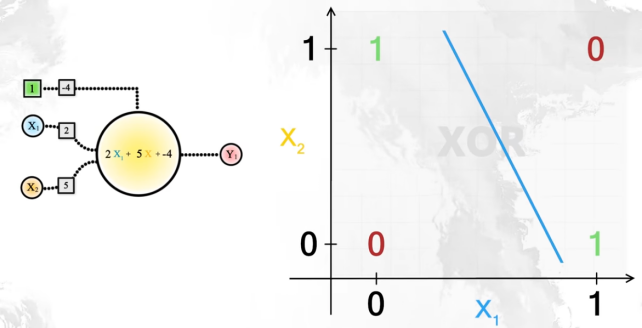
Para logralo necesitaríamos dos neuronas:
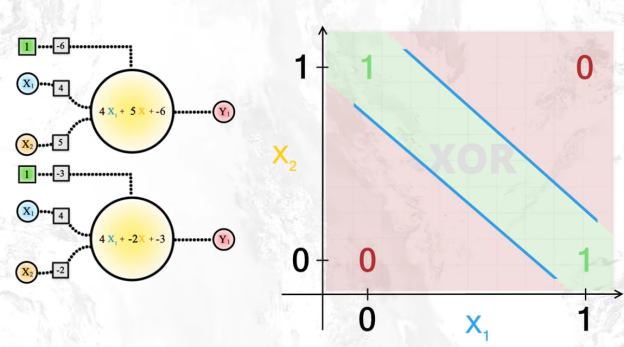
Por lo tanto, uniendo más neuronas conseguiremos modelos más complejos.
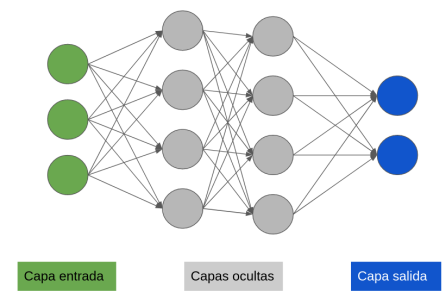
Está formada por capas de neuronas donde las neuronas de una capa se relacionan con las de la siguiente:
Sin embargo, si combinamos capas de regresión lineal nos da como resultado sólo una regresión lineal, es como si sólo hubiésemos hecho una operación, equivaldría a tener sólo una neurona:
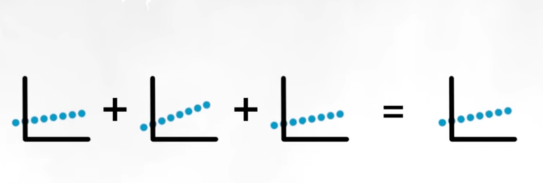
Por lo tanto, necesitaremos manipular cada línea que dé como resultado funciones no lineales obteniendo un resultado final no lineal:

Para conseguir esa no linealidad usaremos las funciones de activación:
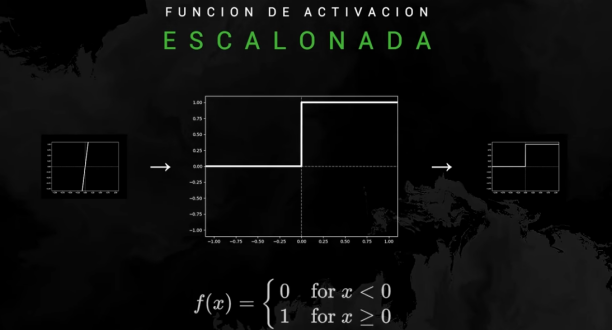
Puece ser una función escalonada, como la usada en el ejemplo de la neurona:
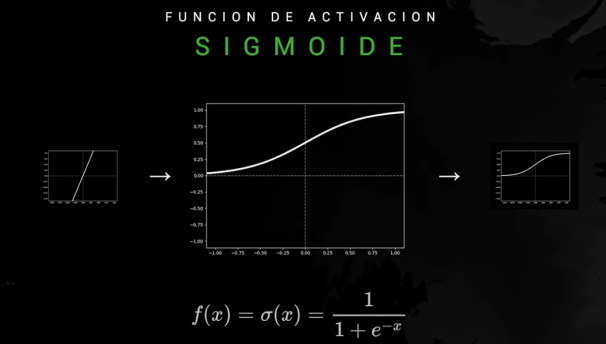
Función sigmoide: tiene valores entre 0 y 1 por lo que es útil para representar probabilidades.
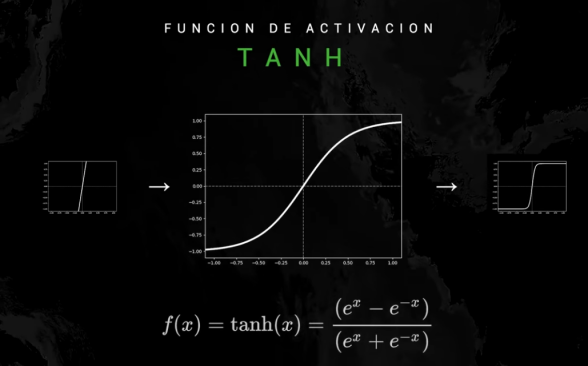
Función tangente hiperbólica: similar a la sigmoide pero con valores entre -1 y 1:
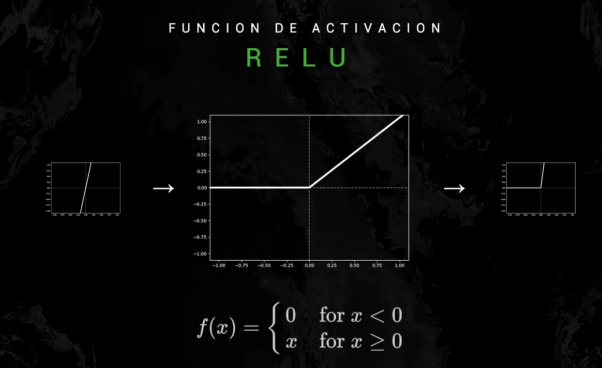
Función unidad rectificada lineal (ReLU): da 0 cuando la entrada es negativa. Es muy utilizada.
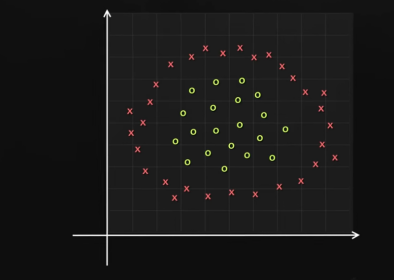
Ahora uniendo diferentes neuronas con sus funciones de activación podemos solucionar problemas más complejos, como clasificar los puntos dentro de un círculo:
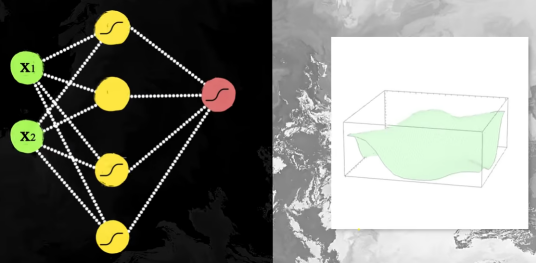
Colocando 4 neuronas con las funciones de activación orientadas de forma distinta:

Nos da como resultado una firgura con un bulto encima:
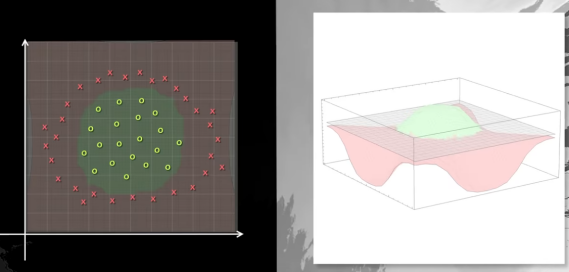
Que será la solución a nuestro problema:
Ahora que ya tenemos el modelo,veamos cómo aprende automáticamente.
Queremos que sea la red la que ajuste automáticamente los parámetros para solucionar el problema.
Se calcula el error final de la red y se recorre cada capa empezando por la última y repartiendo ese error entre las neuronas de la capa anterior. Esos errores se usarán para calcular el gradiente de cada parámetro de la red.
Este gradiente será usado por el algoritmo del descenso del gradiente, que irá ajustando los parámetros en busca del error mínimo.
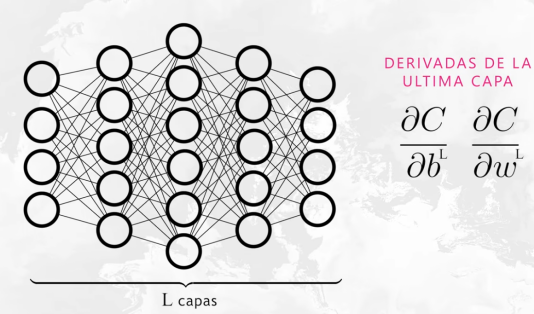
Se realizarán las derivadas del coste respecto de cada peso y del sesgo (b):

La función de coste es la composición de las siguientes funciones:
- Suma ponderada de parámetros (w y b) y el valor de la función de activación de la capa anterior(a)
- Función de activación (a)
- Función de coste (error) (C)

Para realizar el cálculo usamos la regla de la cadena:




Para ver cuanto afecta en el coste un cambio en la neurona, cuanta responsabilidad tiene en el coste final, tenemos esto:
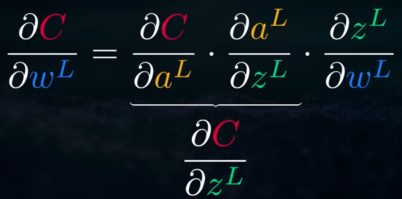

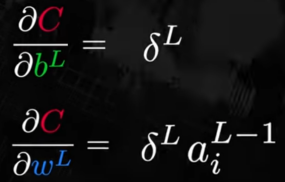
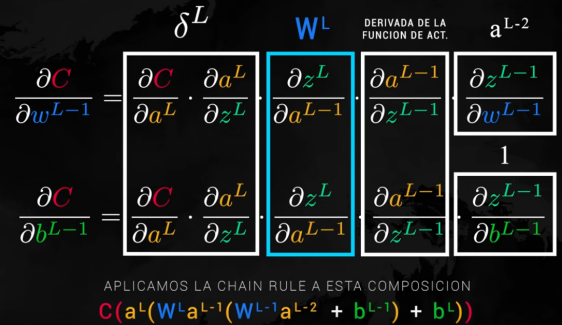

Al final realizaremos estos 3 pasos:

Por lo tanto, con un único pase hacia atrás podemos calcular las derivadas parciales de toda la red. Repartimos el error de la capa siguiente (l) en la capa actual (l-1).
Estas derivadas paraciales se usarán en el descenso del gradiente para encontrar la solución del problema con mínimo error.